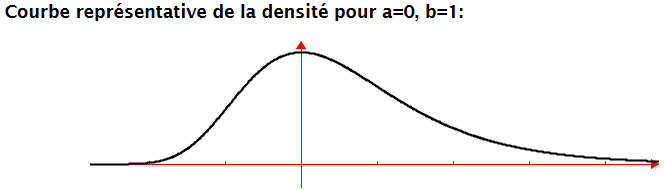
Loi de Gumbel de paramètres \(a\) et \(b\)
Loi de probabilité donc la
Densité est : $$f(x)=\frac1be^{-e^{-(x-a)/b} }e^{-(x-a)/b}$$
- espérance : \({\Bbb E}[X]=\) \(a+b\gamma\), où \(\gamma\) est la Constante d'Euler
- variance : \(V(x)=\) \(\frac{\pi^2b^2}6\)
- fonction de répartition : $$F(x)=e^{-e^{-(x-a)/b} }$$
- signification : est très utilisée en hydrologie et en climatologie pour estimer les valeurs extrêmes des phénomènes
- si des variables aléatoires indépendantes suivent la Loi normale centrée réduite, leur maximum suit, pour \(n\) grand, la loi de Gumbel de paramètres \((a,b)=\) \((\sqrt{2\ln(n)},\frac1{\sqrt{2\ln(n)} })\)
